算法图解
算法简介
对数
对数运算是幂运算的逆运算。

二分查找如何实现
def binary_search(array,item):
low = 0
high = len(array) - 1
print("large index is %d"%high)
while low <= high:
mid = int((low + high)/2)
guess = array[mid]
print("Mid is %d"%mid)
print("guess is %d"%guess)
if guess == item:
return mid
elif guess < item:
low = mid + 1
print("+++++++low is %d"%low)
elif guess > item:
high = mid - 1
print("-------high is %d"%high)
else:
return None
myList = [1,3,7,9,12,23,45,67,89,123,244,345,456,1234]
print(binary_search(myList,23))
运行时间
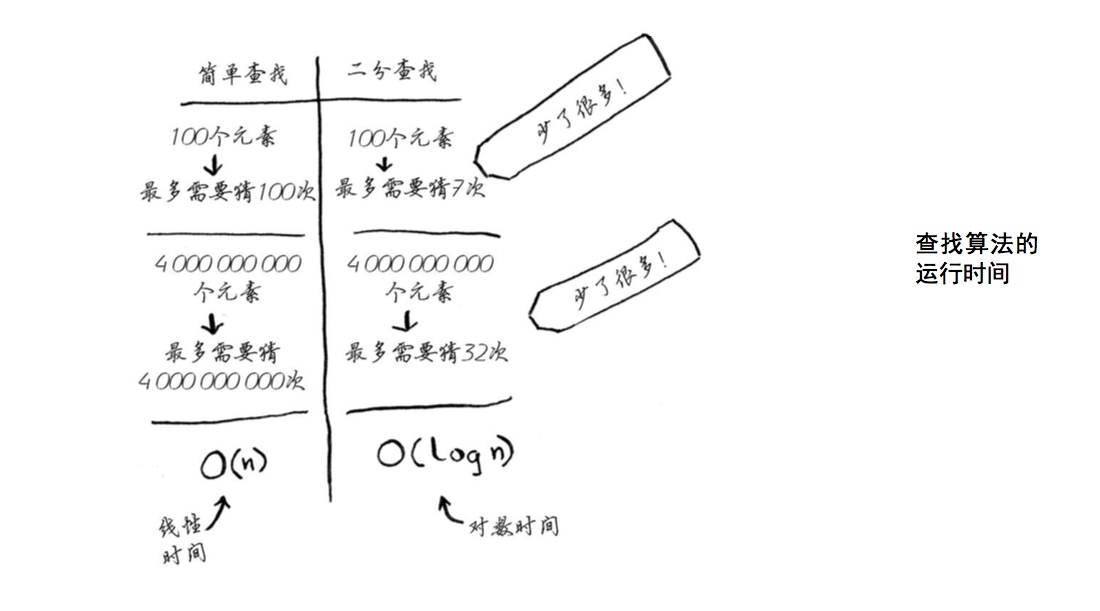
每次介绍算法时,我都将讨论其运行时间。一般而言,应选择效率最高的算 法,以最大限度地减少运行时间或占用空间。 简单查找逐个地检查数 字,如果列表包含100个数字,最多需要猜100次。如果列表包含40亿个数字,最 多需要猜40亿次。换言之,最多需要猜测的次数与列表长度相同,这被称为线性 时间(linear time)。 二分查找则不同。如果列表包含100个元素,最多要猜7次;如果列表包含40亿个数字,最多 需猜32次。厉害吧?二分查找的运行时间为对数时间(或log时间)。
大 O 表示法
- 大O表示法是一种特殊的表示法,指出了算法的速度有多快。
- 大O表示法 让你能够比较操作数,它指出了算法运行时间的增速。
- 大O表示法指出了最糟情况下的运行时间。
- 算法的速度指的并非时间,而是操作数的增速。
- 谈论算法的速度时,我们说的是随着输入的增加,其运行时间将以什么样的速度增加。
- 算法的运行时间用大O表示法表示。
- O(log n)比O(n)快,当需要搜索的元素越多时,前者比后者快得越多
下面按从快到慢的顺序列出了经常会遇到的5种大O运行时间。
- O(log n),也叫对数时间,这样的算法包括二分查找。
- O(n),也叫线性时间,这样的算法包括简单查找。
- O(n * log n),这样的算法包括第4章将介绍的快速排序——一种速度较快的排序算法。
- O(n2),这样的算法包括第2章将介绍的选择排序——一种速度较慢的排序算法。
- O(n!),这样的算法包括接下来将介绍的旅行商问题的解决方案——一种非常慢的算法。
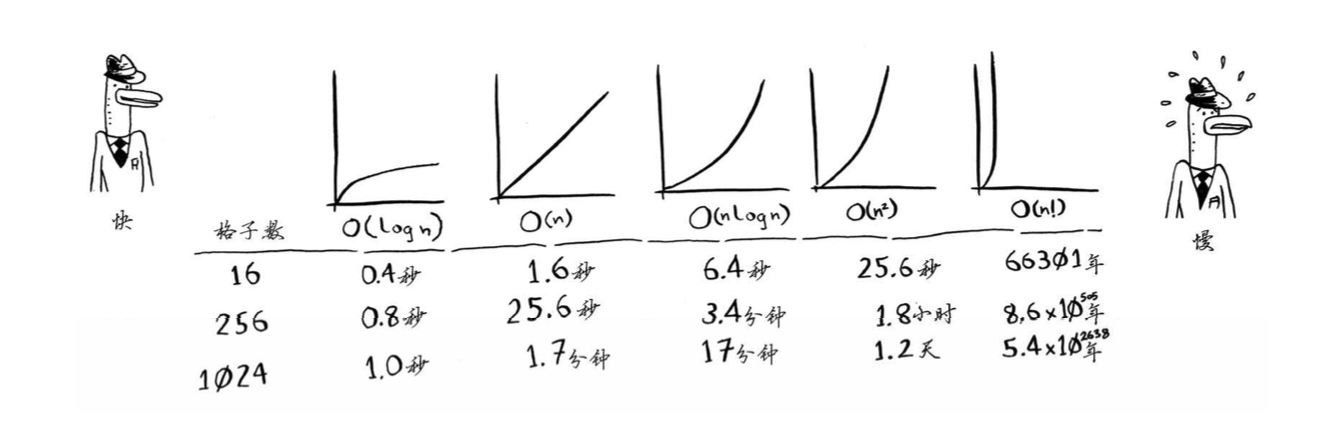
选择排序
内存的工作原理
假设你去看演出,需要将东西寄存。寄存处有一个柜子,柜子有很多抽屉。 每个抽屉可放一样东西,你有两样东西要寄存,因此要了两个抽屉。 你将两样东西存放在这里。 现在你可以去看演出了!这大致就是计算机内存的工作原理。计算机就像是很多抽屉的集合体,每个抽屉都有地址。 需要将数据存储到内存时,你请求计算机提供存储空间,计算机给你一个存储地址。需要存储多项数据时,有两种基本方式——数组和链表。但它们并非都适用于所有的情形,因此知道它们的差别很重要。
数组和链表
- 数组 :所有元素在内存中都是相连的,添加需要重新申请内存。
- 链表 :链表中的元素可存储在内存的任何地方。链表的每个元素都存储了下一个元素的地址,从而使一系列随机的内存地址串在一起。使用链表时,根本就不需要移动元素。链表的优势在插入元素方面。
- 插入元素:使用链表时,只需要修改前面那个元素指向的地址就可以插入元素,数组的话,就需要把元素后面的元素全部向后移动,如果没有足够的时间的话,还得将数组复制到其他地方。
- 删除元素:使用链表时,只需要修改前一个元素指向的地址就行了,使用数组的话,删除元素后面的元素都需要向前移。
| 优点 | 缺点 | |
|---|---|---|
| 数组 | 查找方便 | 必须使用连续的存储空间,添加元素需要从新分配内存 |
| 链表 | 可以使用分割开的内存,添加元素方便 | 查找慢,必须重头开始一个个地址的查。 |
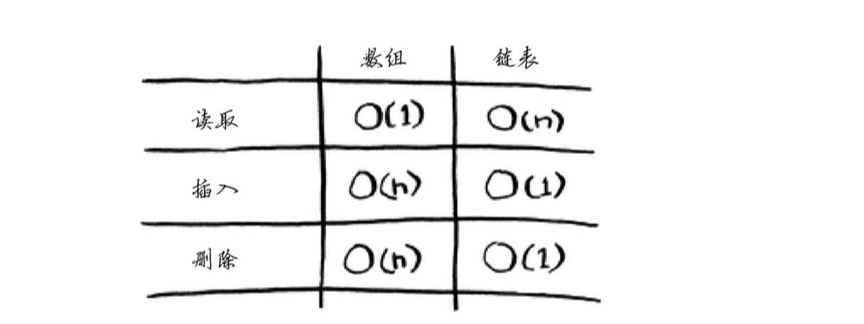
常见的数组和链表操作的运行时间
选择排序
时间:O(n²)
# 找出当前数组最小的数字的index
def findSmallest(arr):
smallest = arr[0]
smallest_index = 0
for i in range(1,len(arr)):
if arr[i] < smallest:
smallest = arr[i]
smallest_index = i
return smallest_index
# 选择排序 O(n²)
def selectionSort(arr):
newArr = []
for i in range(len(arr)):
smallest_index = findSmallest(arr)
# arr.pop(smallest_index) 移除指定位置的元素,并返回这个元素
newArr.append(arr.pop(smallest_index))
return newArr
print (selectionSort([5, 3, 6, 2, 10]))
小结
- 计算机内存犹如一大堆抽屉。
- 需要存储多个元素时,可使用数组或链表。
- 数组的元素都在一起。
- 链表的元素是分开的,其中每个元素都存储了下一个元素的地址。
- 数组的读取速度很快。
- 链表的插入和删除速度很快。
- 在同一个数组中,所有元素的类型都必须相同(都为int、double等)。
递归
编写递归函数时,必须告诉它何时停止递归。正因为如此,每个递归函数都有两部分:基线 条件(base case)和递归条件(recursive case)。递归条件指的是函数调用自己,而基线条件则 指的是函数不再调用自己,从而避免形成无限循环。

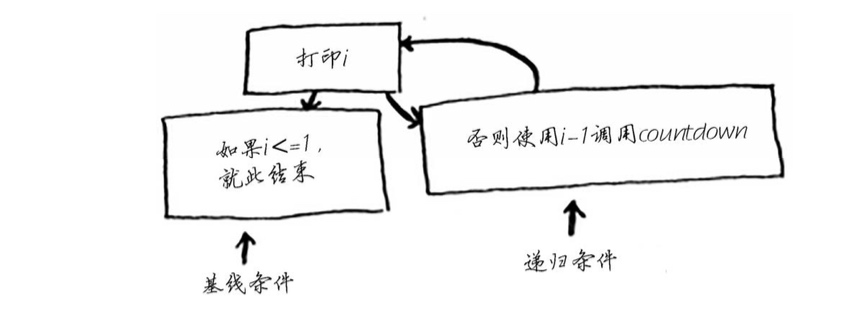
栈
调用栈
计算机在内部使用被称为调用栈的栈。 下面是一个 简单的函数。
def greet(name):
print "hello, " + name + "!"
greet2(name)
print "getting ready to say bye..."
bye()
这个函数问候用户,再调用另外两个函数。这两个函数的代码如下。
def greet2(name):
print "how are you, " + name + "?"
def bye():
print "ok bye!"
假设你调用greet(“maggie”),计算机将首先为该函数调用分配一块内存。
我们来使用这些内存。变量name被设置为maggie,这需要存储到内存中。
每当你调用函数时,计算机都像这样将函数调用涉及的所有变量的值存储到内存中。接下来, 你打印hello, maggie!,再调用greet2(“maggie”)。同样,计算机也为这个函数调用分配一 块内存。
计算机使用一个栈来表示这些内存块,其中第二个内存块位于第一个内存块上面。你打印 how are you, maggie?,然后从函数调用返回。此时,栈顶的内存块被弹出。
现在,栈顶的内存块是函数greet的,这意味着你返回到了函数greet。当你调用函数greet2 时,函数greet只执行了一部分。这是本节的一个重要概念:调用另一个函数时,当前函数暂停 并处于未完成状态。该函数的所有变量的值都还在内存中。执行完函数greet2后,你回到函数 greet,并从离开的地方开始接着往下执行:首先打印getting ready to say bye…,再调用 函数bye。
在栈顶添加了函数bye的内存块。然后,你打印ok bye!,并从这个函数返回。
现在你又回到了函数greet。由于没有别的事情要做,你就从函数greet返回。这个栈用于 存储多个函数的变量,被称为调用栈。
这一段讲的真好,之前一直理不清楚这个概念
小结
- 递归指的是调用自己的函数。
- 每个递归函数都有两个条件:基线条件和递归条件。 * 栈有两种操作:压入和弹出。
- 所有函数调用都进入调用栈。
- 调用栈可能很长,这将占用大量的内存。
快速排序
分而治之(divide(划分) and conquer(征服))
D&C的工作原理:
- 找出简单的基线条件;
- 确定如何缩小问题的规模,使其符合基线条件。
快速排序
- 快速排序是一种常用的排序算法,比选择排序快得多。
- 例如,C语言标准库中的函数qsort 实现的就是快速排序。
- 快速排序也使用了D&C。
- 基线条件
- 基线条件为数组为空或只包含一个元素。在这种情况下,只需原样返回数组——根本就不用排序。
- 缩小问题规模
- 首先,从数组中选择一个元素,这个元素被称为基准值(pivot)。
- 接下来,找出比基准值小的元素以及比基准值大的元素。
- 这被称为分区(partitioning)
- 基线条件
代码实现如下:
# 这样写更好理解一点
def quickSort(array):
# 判断数组是否满足基线条件,如果满足基线条件直接返回
# 如果不满足基线条件,继续减小问题规模
if len(array) > 1:
mid = array[0]
largeArray = []
smallArray = []
print("---------------mid = " + str(mid))
for index in range(1,len(array)):
value = array[index]
if value > mid :
largeArray = largeArray +[value]
else :
smallArray = smallArray +[value]
print("smallArrar = " + str(smallArray))
print("largeArray = " + str(largeArray))
return quickSort(smallArray) + [mid] + quickSort(largeArray)
else:
return array
#更符合 Python 的写法
def quicksort(array):
if len(array) < 2:
# base case, arrays with 0 or 1 element are already "sorted"
return array
else:
# recursive case
pivot = array[0]
# sub-array of all the elements less than the pivot
less = [i for i in array[1:] if i <= pivot]
# sub-array of all the elements greater than the pivot
greater = [i for i in array[1:] if i > pivot]
return quicksort(less) + [pivot] + quicksort(greater)
这行代码的意思:
less = [i for i in array[1:] if i <= pivot]
寻找 array 中 index 1 到末尾的元素,当这个元素小于等于 pivot 时,返回这个元素 i,存储在数组中;
图形演示更直观一点:
推荐一个网站visualgo,可以直观的演示算法的执行过程。
为什么快速排序的复杂度为 n*log n
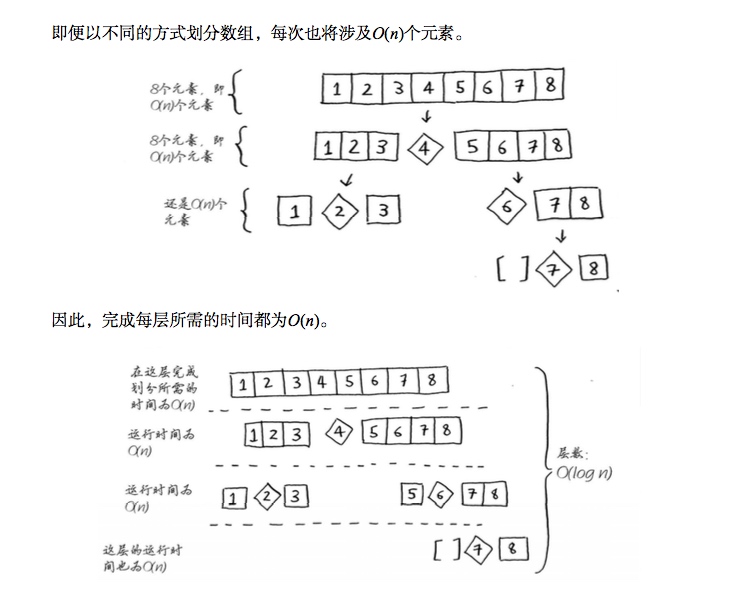
在这个示例中,层数为O(log n)(用技术术语说,调用栈的高度为O(log n)),而每层需要的 时间O(n)。因此整个算法需要的时间为O(n) * O(log n) = O(n log n)。这就是最佳情况。 在最糟情况下,有O(n)层,因此该算法的运行时间为O(n) * O(n) = O(n²)。 只要你每次都随机地选择一个数组元素作为基准值,快速排序的平均运行时间就将为O(n log n)。快速排序是最快的排序算法之一,也是D&C典范.
散列表
散列表 哈希表 字典 区别与共同点
散列表查找速度是 O(1)。
散列函数
散列函数是这样的函数,即无论你给它什么数据,它都还你一个数字.
散列函数必须满足一些要求:
- 它必须是一致的。输入相同的内容时,得到是数字是一样的。
- 它应将不同的输入映射到不同的数字。例如,如果一个散列函数不管输入是什么都返回1, 它就不是好的散列函数。最理想的情况是,将不同的输入映射到不同的数字。
散列函数为什么可以迅速查找到结果:
- 散列函数总是将同样的输入映射到相同的索引。每次你输入avocado,得到的都是同一个 数字。因此,你可首先使用它来确定将鳄梨的价格存储在什么地方,并在以后使用它来 确定鳄梨的价格存储在什么地方。
- 散列函数将不同的输入映射到不同的索引。。avocado映射到索引4,milk映射到索引0。每 种商品都映射到数组的不同位置,让你能够将其价格存储到这里。
- 散列函数知道数组有多大,只返回有效的索引。如果数组包含5个元素,散列函数就不会 返回无效索引100。
散列表应用
- 用于查找
- 无论你访问哪个网站,其网址都必须转换为IP地址。这个过程被称为DNS解析 (DNS resolution),散列表是提供这种功能的方式之一。
- 防止重复
- 用作缓存
- 缓存是一种常用的加速方式,所有大型网站都使用缓存,而缓存的数据则存储在散列表中!
小结
- 可以结合散列函数和数组来创建散列表。
- 冲突很糟糕,你应使用可以最大限度减少冲突的散列函数。
- 散列表的查找、插入和删除速度都非常快。
- 散列表适合用于模拟映射关系。
- 一旦填装因子超过0.7,就该调整散列表的长度。
- 散列表可用于缓存数据(例如,在Web服务器上)。
- 散列表非常适合用于防止重复。
广度优先搜索
广度优先搜索让你能够找出两样东西之间的最短距离,不过最短距离的含义有很多!使用广 度优先搜索可以:
- 编写国际跳棋AI,计算最少走多少步就可获胜;
- 编写拼写检查器,计算最少编辑多少个地方就可将错拼的单词改成正确的单词,如将 READED改为READER需要编辑一个地方;
- 根据你的人际关系网络找到关系最近的医生。
解决最短路径问题的算法被称为广度优先搜索。
图简介
图由节点和边组成。一个节点可能与众多节点直接相连,这些节点被称为邻居。
图模拟一组连接。
图用于模拟不同的东西是如何相连的。
广度优先搜索
广度优先搜索可回答两类问题:
- 第一类问题:从节点A出发,有前往节点B的路径吗?
- 第二类问题:从节点A出发,前往节点B的哪条路径最短?
假设 需要查找 你认识的人中,以及你认识的人所认识的人中,是否有名字末尾为 M 的人。
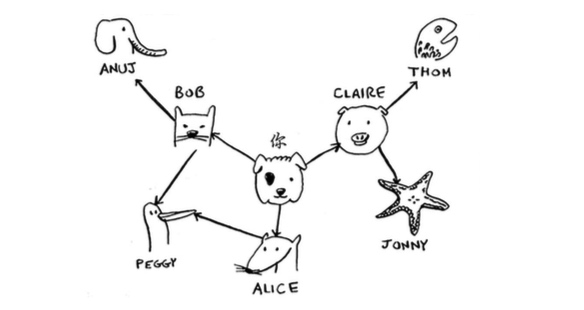
搜索的步骤:
- 先查看 你 认识的人中是否有符合条件的人;
- 找到 alice、bob、claire 三个人
- 如果有直接返回这个人,如果没有,就继续查找你认识的人中的社交关系是否有需要查找的人。
- 这三个人没有一个符合条件的人,把他们加入到队列中
- 从队列中取出候选人查看,如果候选人不符合,就把候选人的联系人继续添加到队列中,同时标识这个候选人已经排查过了。
- 知道找到需要的人,或者整个社交圈搜索完毕。
- 重复上面的操作。
具体实现如下:
from collections import deque
graph = {}
graph["you"] = ["alice", "bob", "claire"]
graph["bob"] = ["anuj", "peggy"]
graph["alice"] = ["peggy"]
graph["claire"] = ["thom", "jonny"]
graph["anuj"] = []
graph["peggy"] = []
graph["thom"] = []
graph["jonny"] = []
# 判断是不是需要找到的人
def person_is_seller(name):
if name[-1] == 'm':
return True
else:
return False
# 查找与 name 关系最近的符合条件的人
def searchName(name):
# 创建一个队列 用于存储要查找的人
searchQueue = deque()
# 先在 name 的第一层级去找是否有符合条件的人
searchQueue += graph[name]
# 用于记录 已经查找过的人 放置重复查找
searched = []
# 当队列不为空时,循环执行
while searchQueue:
# 取出队列的第一个人
person = searchQueue.popleft()
# 当前 person 没有被查找过
if not person in searched:
print("searching " + person)
# 判断 person 是否我们需要的人。
if person_is_seller(person):
print(person + " is you need person")
return True
else:
# 如果 person 不是符合条件的人
# 把与 person 关联的人加入到队列中
searchQueue += graph[person]
# 把 person 标记为已经查找过
searched.append(person)
return False
# 查找跟 “you” 关系最近发符合条件的人。
searchName("you")
狄克斯特拉算法
狄克斯特拉算法 找出最快路径。
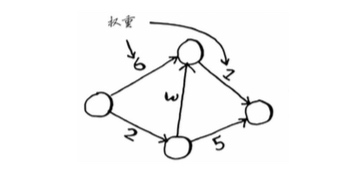
狄克斯特拉算法用于每条边都有关联数字的图,这些数字称为权重(weight)。
狄克斯特拉算法只适用于有向无环图(directed acyclic graph,DAG)。
带权重的图称为 加权图(weighted graph),不带权重的图称为 非加权图(unweighted graph)。
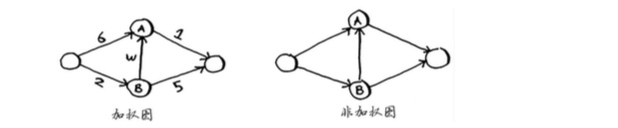
要计算非加权图中的最短路径,可使用广度优先搜索。要计算加权图中的最短路径,可使用狄克斯特拉算法。
狄克斯特拉算法包含4个步骤:
- 找出“最便宜”的节点,即可在最短时间内到达的节点。
- 更新该节点的邻居的开销,其含义将稍后介绍。
- 重复这个过程,直到对图中的每个节点都这样做了。
- 计算最终路径。